Underneath Modern Cryptography : Introduction to Elliptic Curves
Why do we care so much about cryptograhy?
Cryptography is the guardian of our digital world. It keeps our data, identities, and communications safe in an era of constant connectivity. Without it, our online lives would be vulnerable to cyber threats and privacy breaches. In essence, cryptography is the bedrock of trust in the digital age, ensuring our security and privacy online.
Let’s get few basics cleared up
Cryptography is basically based on a mathematical problem which is very hard to be solved by computers. Cryptography is a field that deals with securing information by converting it into a form that is unintelligible to unauthorized individuals. The basis of cryptography lies in the use of mathematical algorithms and techniques to protect data confidentiality, integrity, and authenticity.
The strength of cryptography lies in the fact that these mathematical problems are computationally hard to solve. For example, factoring large numbers into their prime factors is a time-consuming task for classical computers, especially when dealing with extremely large numbers. This difficulty forms the basis of many cryptographic algorithms, making it infeasible for an attacker to reverse-engineer the original message from the ciphertext without knowledge of the secret key.
Like the prime numbers we talked about, in cryptography we don’t deal with our usual number system, rather we operate within mathematical groups. A group is a set of elements with a binary operation that satisfies a few set of properties. Majority of the algorithms use what we know as the multiplicative group $\mathbb G$ of integers modulo a sufficiently large prime $p$.
So why groups suddenly, leaving our normal number system? For this we need to understand about the Discrete Logarithm Problem (DLP). The DLP is the basis of many cryptographic algorithms, including the Diffie-Hellman key exchange, ElGamal encryption, and the Digital Signature Algorithm (DSA). But more on that later.
Modern cryptography often uses groups, instead of the normal number system (integers) because these groups offer specific mathematical properties that make encryption and security algorithms more robust against attacks, including the difficulty of solving certain mathematical problems, like the discrete logarithm problem, which underlie many cryptographic schemes. These groups provide a foundation for building secure encryption and digital signature systems. And modern cryptography specifically use what we call Elliptic Curve Groups. So let’s have a dive into this modern cryptography, but before that let’s understand what are two of the most important problems in cryptography.
The Discrete Logarithm Problem
The discrete logarithm problem is a fundamental mathematical problem in the field of number theory and plays a central role in modern cryptography, particularly in the security of public-key cryptosystems. The discrete logarithm problem is defined as for a given group $\mathbb G$ with generator $g$ and an element $h \in \mathbb G$. $\mathbb{G}$ is a multiplicative group.
\[\mathbb{G} : \{1, g, g^2, g^3, \ldots, g^{p-1}\}\]Now the problem says, the follows
\[\text{given} \: y \in \mathbb{G}, \: \text{find} \: x \: \text{such} \: \text{that} \: g^x = y \\ \text{Example : Find } x \: \text{such that } 3^x = 4 \: \text{mod} \: 7\]Here finding $x$ is the discrete logarithm problem. The discrete logarithm problem is considered to be computationally infeasible. This means that it is believed that no efficient algorithm exists for computing discrete logarithms in general.
The Computational Diffie-Hellman Assumtion
The Computational Diffie-Hellman Assumption (CDH) is a foundational assumption in cryptography, particularly in the context of the Diffie-Hellman key exchange protocol and related cryptographic systems. This assumption forms the basis for the security of many encryption and key exchange schemes.
This is like an extension to the Discrete Logarithm Problem. The CDH problem is defined as follows: given a group $\mathbb{G}$ with generator $g$ and elements $g^a$ and $g^b$, find $g^{ab}$.
Elliptic Curve Cryptography (ECC)
Our primary example for the group $\mathbb G$ was the multiplicative group (or subgroup) of integers modulo a sufficiently large prime $p$. This group is problematic for a number of reasons, most notably because the discrete log problem in this group is not sufficiently difficult. The best known algorithm, called the general number field sieve (GNFS). It was used in 2019 to solve a discrete log problem modulo a general 795-bit prime. This algorithm is the reason why, in practice, we must use a prime $p$ whose size is at least 2048 bits. High security applications must use even larger primes. Arithmetic modulo such large primes is slow and greatly increases the cost of deploying cryptosystems that use this group.
Several other families of finite cyclic groups with an apparent hard discrete log have been proposed. Of all these proposals, the group of points of an elliptic curve over a prime finite field is the most suitable for practice, and is widely used on the Internet today. Also because ECC offers same security as of RSA in much smaller key sizes. You can see the significant improvemence in using Elliptic Curves over traditional RSA/AES.\
| Key Size | ECC | RSA |
|---|---|---|
| 80 | 163 | 1024 |
| 128 | 283 | 3072 |
| 256 | 571 | 15360 |
By leveraging the difficulty of solving certain mathematical problems on elliptic curves, cryptographic systems can ensure the confidentiality and integrity of sensitive information. The use of elliptic curves in cryptography has gained significant attention due to their efficiency and robustness, making them a cornerstone of modern secure communication.
In short we can see it like a special group of points on a plane, which satisfy a certain mathematical equation. The equation is of the form
\[y^2 = x^3 + ax + b, \: \text{satisfys} \:\: 4a^3 + 27b^2 \neq 0\]Here you can have 2 elliptic curve elements $P \in G$ & $Q \in G$ and you can add them to get a new element $R \in G$. The defination of addition method over this group, can be seen diagrammatically below
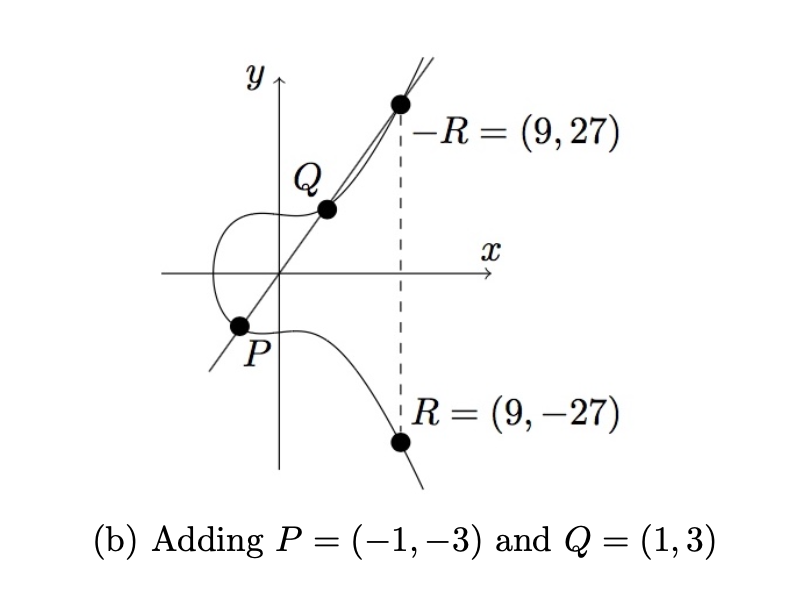
You can multiply an element $g \in G$ with a scalar $a \in \mathbb F_p$, where $p$ is the curve order of group $G : h=ag$. This is called scalar multiplication. There is no way to compute the product of two curve elements: the operation $g_1 \ast g_2$ is not defined, as opposed to multiplying by a scalar.
Another important property is that there is no efficient algorithm to compute discrete logarithms. The meaning of this is that given $h$ and $g$ with the property that $h=ag$, if you don’t know $a$ it is computationally infeasible to find $a$.
The equation mentioned about is called the Weierstrass equation. There are other forms of the equation, like the Montgomery form and the Edwards form, and also the twisted Edwards form.
Edwards Curves. Another way to describe an elliptic curve $E/\mathbb{E_p}$ is in Edwards form, which is
where $d \in \mathbb{F_p}$ satisfies $d \neq 0,1$. Again, this curve can be put into Weierstrass form via a simple rational change of variable. The beauty of the Edwards form is that the chord and tangent addition law is extremely easy to describe. For points $P = (x_1,y_1)$ and $Q = (x_2, _y2)$ in $E(\mathbb F_p)$, we define
\[P \boxplus Q := \bigg(\frac{x_1y_2 + x_2y_1}{1+dx_1x_2y_1y_2}, \frac{y_1y_2 - x_1x_2}{1-dx_1x_2y_1y_2} \bigg)\]Let $E/\mathbb{F_p}$ be an elliptic curve and let $E(\mathbb{F_p})$ be the group of points on this curve that are defined over $\mathbb{F_p}$. We know that $E(\mathbb{F_p})$ is a finite abelian group. Suppose that it also happens to be cyclic, meaning that $E(\mathbb{F_p})$ is generated by some point $P \in E(\mathbb{F_p})$. We can now ask about the complexity of problems like discrete log, computational Diffie-Hellman (CDH), and decision Diffie-Hellman (DDH) in the group $E(\mathbb{F_p})$. The resulting systems are called elliptic curve cryptosystems.
As we will see, certain elliptic curve groups have an additional structure, called a pairing, that is enormously useful in cryptography. We will see many examples of encryption and signature schemes built using pairings. These systems exhibit powerful properties that are beyond what can be built using the multiplicative group of the integers modulo a prime. Some examples include aggregate signatures, broadcast encryption, functional encryption, and many others. Up until now, we used elliptic curves as an efficient group where the discrete log problem and its variants, CDH and DDH, are believed to be difficult.
This group makes it possible to instantiate efficiently many of the schemes described in earlier chapters. We now show that certain elliptic curves have an additional structure, called a pairing. The pairing enables a world of new schemes that could not be built from discrete log groups without this additional structure. The resulting schemes make up an important area called pairing based cryptography. Why pairing is so important ? This is because with pairing we cannot break the CDH assumption i.e cannot compute $g^{xy}$. But given the value of $g^{xy}$ as $h$, then we can check if it is true or not. This opens up the door to Zero-Knowledge Cryptography