Journey into the Cryptographic Rabbithole
As the last week I decided to work in the Verkle Tree implementation, this week have been a really good learning experience. I have been reading a lot of papers and blogs about the implementation of the Verkle Tree, and also the different cryptographic primitives that are used in the implementation. In summary this week the followings were done : -
- Elliptic Curves & cryptography based along with different curve implementations.
- Pairings based on elliptic curves, and the different pairings like Weil & Tate Pairing
- Bandersnatch Curve and Banderwagon built on top of BLS12_381 curve.
- Talking with @zahary about the project proposal and how to go about the implementation in Nim.
Learnings
Elliptic curves are a fundamental concept in modern cryptography and mathematics. In the context of the conversation, elliptic curves play a crucial role in secure communication protocols and encryption algorithms. These curves are defined by a mathematical equation and possess unique properties that make them suitable for cryptographic applications. By leveraging the difficulty of solving certain mathematical problems on elliptic curves, cryptographic systems can ensure the confidentiality and integrity of sensitive information. The use of elliptic curves in cryptography has gained significant attention due to their efficiency and robustness, making them a cornerstone of modern secure communication.
In short we can see it like a special group of points on a plane, which satisfy a certain mathematical equation. The equation is of the form
\[y^2 = x^3 + ax + b, \: \text{satisfys} \:\: 4a^3 + 27b^2 \neq 0\]Here you can have 2 elliptic curve elements $P \in G$ & $Q \in G$ and you can add them to get a new element $R \in G$. The defination of addition method over this group, can be seen diagrammatically below
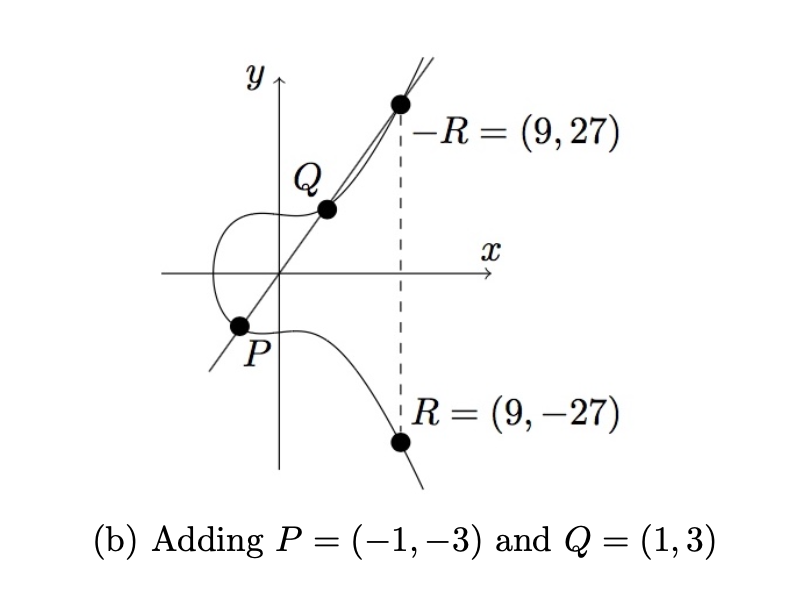
You can multiply an element $g \in G$ with a scalar $a \in \mathbb F_p$, where $p$ is the curve order of group $G : h=ag$. This is called scalar multiplication. There is no way to compute the product of two curve elements: the operation $g_1 \ast g_2$ is not defined, as opposed to multiplying by a scalar.
Another important property is that there is no efficient algorithm to compute discrete logarithms. The meaning of this is that given $h$ and $g$ with the property that $h=ag$, if you don’t know $a$ it is computationally infeasible to find $a$.
The equation mentioned about is called the Weierstrass equation. There are other forms of the equation, like the Montgomery form and the Edwards form, and also the twisted Edwards form.

This understanding of Elliptic Curves is gave me more clarity on the polynomial commitments and it’s interface implementations, like keygen, commit, open, verify, etc.
Why all this was required? This was because the Verkle Tree implementation relies on polynomial commitments which are based on elliptic curves. According to the different implementations that I have seen and the standards layed out by the Ethereum Foundation we would be using the Banderwagon Curve, this is built on top of Bandersnatch Curve to solve the cofactor issue of Twisted Edward curves. Haven’t dived very deep into the Banderwagon yet, would do if required. I did see the performance optimizations of Bandersnatch over other elliptic curves for example
| Curve | Cost |
|---|---|
| Jubjub | $75\mu$ |
| Bandersnatch | $44\mu$ |
| Improvement | $42\%$ |
Discussion with Nimbus Team
A meeting was scheduled with @zahary and the Nimbus team, but due to some issue it got delayed and we had a discussion on the Nimbus channel. The discussion was about the project proposal and how to go about the implementation in Nim. Now the meeting agenda would be to spec out the development process on the high level, and also to discuss the different cryptographic primitives that would be required and are available in Nim, or can be ported to Nim using nbindgen.
Despite of the delay, my talk with mentor progessed and got a very rough idea of how they are trying to move forward with their implementation. They did start the development work around a week ago, as I saw a few commits in the Verkle Tree repo in the github of Status. I was trying to understand it, and found that they were playing around a bit with KZG implementation available in Ethereum github, couldn’t understand why they are interested in KZG, as the standard for the Verkle Tree implementation is IPA. I would be discussing this with them in the meeting, and would try to understand their thought process behind this.